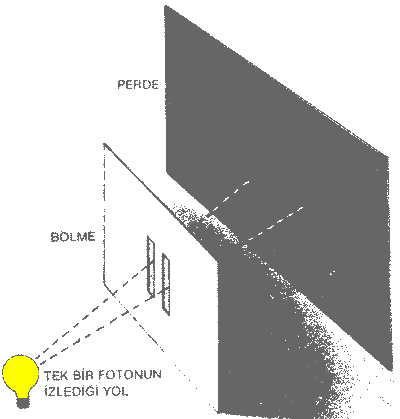
Belirsizlik İlkesi

Bilimsel kuramların, özellikle Newton'm çekim yasasının başarısı, ondokuzuncu yüzyılın başında Fransız bilimcisi Marki Laplace'ı [Laplas] evrenin tümüyle belirlenir olduğu savına vardırdı. Laplace'ın önerdiğine göre, öyle bir bilimsel yasalar takımı olmalıydı ki, yalnızca bir an için evrenin tümünün durumunu bilirsek evrende olup bitecek her şeyi hesaplayabilirdik, örneğin, güneşin ve gezegenlerin bir andaki hızlarını ve konumlarını biliyorsak, Güneş Sisteminin başka zamanlardaki durumunu Newton'ın yasalarını kullanarak hesaplayabilirdik. Bu bağlamda belirlenirlik oldukça açık gözüküyor ama Laplace bununla kalmayıp insan davranışları da içinde olmak üzere her şeye hükmeden benzeri yasaların varolduğunu ileri sürdu.

Bilimsel belirlenirlik öğretisine, Tanrı'nın dünya işlerine karışma, özgürlüğüne saldırıda bulunduğu için pek çok kişi şiddetle karşı çıktı. Yine de, bu yüzyılın başına dek bilimin olağan bir varsayımı olarak kaldı. Bu inancın terkedilmesi gereğinin ilk göstergesi, Britanyalı bilimciler Lord Rayleigh [Reyli] ve Sir James Jeans'in [Ciyns], sıcak bir nesnenin, ya da yıldız gibi bir cismin sonsuz bir hızda enerji yaydığını ileri sürmeleri oldu. O zaman inandığımız yasalara göre sıcak bir cisim her frekansta eşit bir biçimde elektromanyetik dalgalar (radyo dalgalan, görünen ışık ya da röntgen ışınlan gibi) yaymalıydı. Örneğin sıcak bir cisim, frekansları saniyede bir ile saniyede iki milyon dalga arasındaki dalgalarla yaydığı enerjinin aynısını, frekansları saniyede iki ile üç milyon dalga arasındaki dalgalarla da yayacak. Ama saniyedeki dalga sayısı sınırsız olduğuna göre, yayılan toplam enerji sonsuz olacak demek.

Gülünçlüğü apaçık bu sonuçtan kaçınmak için Alman bilimcisi Max Planck [Plank] 1900'de ışık, röntgen ışınları ve öbür dalgaların herhangi bir sıklıkta değil de, ancak tanecikler diye adlandırdığı belli paketlerle yayılabileceğini öne sürdü Ayrıca, her taneciğin, dalgaların frekansı yükseldikçe artan belli bir enerji vardı. Buna göre, yeterince yüksek bir frekansta, tek bir taneciği yaymak için bile oldukça fazla enerji gerekecek ve böylece yüksek frekanslarda dalga yayını azalacak, yani cisim ancak sonlu bir hızda enerji yitirecekti.

Tanecik varsayımı, sıcak cisimlerden yayılan ışımanın hızını gayet güzel bir biçimde açıklıyordu. Ama bu varsayımın belirlenirliğe etkisi, 1926'da bir başka Alman bilimcisi Werner Heisenberg [Hayzenberg] ünlü belirsizlik ilkesini ortaya koyuncaya dek anlaşılamadı. Bir parçacığın gelecekteki konumunu ve hızını hesaplayabilmek için şu andaki konumunun ve hızının kesin olarak ölçülebilmesi gerekir Bunu yapmanın en kolay yolu parçacığa ışık tutmaktır. Işık dalgalarının bir bölümü parçacığa çarpıp saçılacak ve buradan parçacığın konumu saptanacaktır. Ancak parçacığın konumu, ışığın iki dalga tepesi arasındaki uzaklıktan daha küçük bir hata ile saptanamayacağından, parçacığın konumunu daha kesin ölçmek için daha kısa dalga boylu ışık kullanmak gerekir. İmdi, Planck'ın tanecik varsayımına göre, alabildiğine küçük nicelikte ışık kullanamayız; en az bir adet tanecik kullanmak zorundayız. Bu tek tanecik dokunduğu parçacığın hızını önceden bilinemeyecek bir biçimde değiştirecektir. Üstelik, konumu daha kesin ölçebilmek için daha kısa dalga boylu ışık gerekecek ve bundan dolayı tek bir taneciğin enerjisi daha da yüksek olacaktır. O halde parçacık daha fazla etkilenecektir. Başka deyişle, parçacığın konumunu daha kesin ölçmek için uğraştığınızda, hızını daha hatalı ölçüyor olacaksınız, ya da tersine. Heisenberg gösterdi ki, parçacığın konumundaki belirsizlik ile parçacığın hız çarpı kütlesindeki belirsizliğin çarpımı, Planck sabiti olarak bilinen belli bir nicelikten asla küçük olamaz. Ayrıca, bu sınır koşulu, parçacığın konumunun ya da hızının hangi yolla ölçülmek istendiğine ya da parçacığın türüne bağlı değildir: Heisenberg'in belirsizlik ilkesi dünyanın temel, kaçılamaz bir özelliğidir.

Belirsizlik ilkesi, dünyaya bakış açımıza ta derin den dokunur. Aradan elli yıldan fazla zaman geçmiş olmasına karşın, etkilen çoğu düşünürce kavranamamış olup hala büyük tartışma konusudur.

Belirsizlik ilkesi, Laplace'ın bir bilim kuramı düşünün, tamamıyla belirlenebilir bir evren modelinin ölüm çanını çaldı: eğer evrenin su andaki durumu bile kesin bir biçimde ölçülemiyorsa, gelecekteki olayları doğru hesaplamak hiç mümkün olamazdı! Yine de, hiç bozmadan evrenin şu andaki konumunu gözlemleyebilecek bir doğaüstü varlık için, olayları tümüyle belirleyen bir yasalar takımı olduğunu düşünebiliriz. Ancak, bu türden evren modelleri biz ölümlülere pek ilginç gelmiyor. En iyisi Occam'm tıraş bıçağı denilen tutumluluk ilkesini kullanıp, kuramın gözlemlenemeyen yönlerini kesip atmak. Bu yaklaşım Heisenberg, Erwin Schrödinger [Şrödinger] ve Paul Dirac'ı [Di-rak] 1920lerde mekaniği belirsizlik ilkesi temelinde yeniden ele alıp tanecik mekaniği denilen yeni bir kuram ile açıklamaya götürdü. Bu kuramda parçacıkların iyi tanımlı, ayrı ayrı, ama kesin ölçülemeyen konumları ve hızları yoktu. Bunun yerine, konum ve hızın bileşimi olan bir tanecik durumu vardı.

Genel olarak, tanecik mekaniği bir gözlem için tek ve kesin bir sonuç öngörmez. Bunun yerine, birtakım olası sonuçlar öngörür ve her birinin ne kadar olası olduğunu söyler. Yani, başlangıç durumları aynı bir sürü benzeri sistem için aynı ölçüm yapıldığında, ölçümün sonucu bir bölüm için A. başka bir bölüm için B. vb. bulunur. Sonucun yaklaşık kaçta kaçının A ya da B olacağı hesaplanabilir, ama herhangi bir ölçümün kendine özgü sonucu önceden bilinemez. Tanecik mekaniği böylece bilime kaçınılmaz bir bilinemezlik ya da gelişigüzellik öğesi sokmaktadır. Einstein buna şiddetle karşı çıktı, bu düşüncenin gelişmesinde önemli bir payı bulunduğu halde. Tanecik kuramına katkısından dolayı Einstein'a Nobel ödülü verildi. Buna karşın Einstein evrene şansın hükmettiğini asla kabul etmedi; duyguları şu ünlü deyişiyle özetlenebilir: "Tanrı barbut atmaz." Oysa öbür bilimcilerin çoğu, tanecik mekanikliğini kabul etme yanlısıydılar, çünkü deneylere tamamen uymaktaydı. Gerçekten de, oldukça başarılı bir kuram olarak modern bilim ve teknolojinin neredeyse tümünün temelini oluşturmaktadır. Televizyon ve bilgisayar gibi elektronik aygıtların temel öğeleri olan transistorlar ve tümleşik devrelerin işleyişini, modern kimya ve biyolojinin temelini ona borçluyuz. Tanecik mekaniğini henüz uygun bir biçimde içine alamayan yalnızca iki fizik bilimi alanı, çekim ve evrenin büyük ölçekte yapısı, kaldı.

Işık, dalgalardan oluşmuş olsa bile, Planck'ın tanecik varsayımı bize, bazı yönleriyle ışığın parçacıklardan oluşmuş gibi davrandığını söylüyor: ışık yalnızca paketler, ya da tanecikler biçiminde yayınlanabilir ve soğurabilir. Aynı biçimde, Heisenberg'in belirsizlik ilkesi de parçacıkların bazı yönleriyle dalgalar gibi davranacaklarını anlatıyor: parçacıkların kesin bir konumlarıyoktur ama belli bir olasılık çerçevesinde "dağınık" durumda bulunmaktadırlar. Tanecik mekaniği kuramının dayalı olduğu bu tümüyle yeni matematik temeli, gerçek dünyayı artık parçacıklar ve dalgalar boyutunda açıklamaz; yalnızca gözlemlerimiz bunlarla açıklanabilir. Tanecik mekaniğinde dalgalar ve parçacıklar arasında böyle bir ikilik vardır: bazı durumlarda parçacıkları dalgalar olarak ele almak, öbür durumlarda ise dalgalan parçacıklar olarak ele almak elverişli olmaktadır. Bunun önemli bir sonucu, iki dalga ya da parçacık takımı arasında "girişim" denilen olayın gözlemlenebilmesidir. Yani, bir dalga dizisinin tepeleri öbür dalga dizisinin çukurlarına denk gelir. O zaman bu iki dalga dizisi beklendiği gibi birbirlerine eklenip daha kuvvetli bir dalga oluşturacaklarına, birbirlerini yok ederler (Şekil 4.1). Işık girişiminin bilinen bir örneği, sabun köpükleri üzerinde görülen renklerdir. Bu renklerin nedeni, ışığın, köpüğü oluşturan ince su tabakasının her iki tarafından yansımasıdır. Beyaz ışıkta, hepsi değişik dalga boylu, yani değişik renkli, ışık dalgaları bulunur. Bazı dalga boyları için, sabun tabakasının bir tarafından yansıyan dalgaların tepeleri öbür tarafından yansıyan dalgaların çukurlarına denk düşer. Bu dalga boylarına karşılık olanrenkler yansıyan ışıkta bulunmaz, böylece ışık renkli gözükür.

Girişim olayı parçacıklarda da gözlenir, tanecik mekaniğinin ortaya koyduğu ikilikten ötürü. İyi bilinen bir örnek "iki yarık" denilen deneydir (Şekil 4.2). Üzerinde birbirine koşut iki dar yarık bulunan bir bölme düşünelim. Bölmenin bir yanına belli bir renkte (yani belli bir dalga boyunda) bir ışık kaynağı konmuş olsun. Işığın çoğu bölmeyi aydınlatacak ama az bir bölümü de yarıklardan geçecektir. Bölmenin öbür yanından yeterince uzağa bir perde konmuş olsun. Perdenin üzerindeki herhangi bir noktaya, her iki yarıktan da ışık dalgaları gelecektir. Ancak, genel olarak, ışığın kaynaktan perdeye katettiği yol her iki yarık için değişik olacaktır. Bu demektir ki yarıklardan çıkan dalgalar perdeye vardıklarında aynı fazda olmayacaklardır: bazı yerlerde birbirlerini yok edecekler, bazılarında ise kuvvetlendireceklerdir. Sonuç, kendi ne özgü bir açık/koyu girişim çizgileri şeklidir.

Olağanüstü olan şey, ışık kaynağı yerine belli bir hızı olan (yani belli uzunluktaki dalgalara karşılık olan) parçacıklar, örneğin elektronlar kullanıldığında tıpatıp aynı girişim çizgilerinin elde edileceğidir. Olay daha da bir tuhaf görünebilir, çünkü tek bir yarık durumunda girişim yerine perdenin üzerinde elektronların düzgün bir dağılımı elde edilir. Bir yarık daha açmanın yalnızca perdenin her noktasına düşen elektron sayısını artıracağını düşünmek doğal olabilir, oysa girişim nedeniyle, aslında bu sayı bazı yerlerde azalır. Elektronlar yarıklara tek tek gönderilseler, her biri ya bir yarıktan ya da ötekinden geçecek ve böylece geçtiği yarıktan başka bir tane daha yokmuş gibi davranacak -perdede düzgün bir dağılıma yol açacaktır. Ancak gerçekte, elektronlar tek tek bile gönderilseler girişim çizgileri ortaya çıkmaktadır. O halde her bir elektron her iki yarıktan da aynı anda geçiyor olmalı!

Tanecikler arasındaki girişim olayı, yoldan yola pek değişmeyecek ve bu yollara ilişkin dalgalar yok olmayacaktır. İşte bu yollar, Bohr'un olanaklı yörüngelerine karşılıktır.

Somut matematik biçime konan bu düşüncelerle, daha karmaşık atomlara ve hatta birden çok çekirdek etrafında dönen elektronların bir arada tuttuğu atomlardan oluşan moleküllere ilişkin olanaklı yörüngeleri hesaplamak oldukça, basit bir işleme dönüştü. Moleküllerin yapısı ve birbirleriyle reaksiyonları tüm kimya ve biyolojinin temelini oluşturduğundan, tanecik mekaniği, ilkesel olarak, çevremizde görebildiğimiz hemen her şeyi, belirsizlik ilkesinin çizdiği sınırlar içinde hesaplamamıza olanak sağlar. (Ancak, uygulamada içinde birkaç taneden fazla elektron bulunan dizgeler için gereken hesaplar öylesine karmaşıktır ki, bunu yapamayız.)

Einstein'in genel görelik kuramı evrenin büyük ölçekteki yapısına hükmediyor gibidir. Klasik olarak adlandırılan bir kuramdır; yani tanecik mekaniğinin belirsizlik ilkesini hesaba katmaz, öteki kuramlarla tutarlı olabilmek için gerekse bile. Gözlemlerle herhangi bir çelişkiye düşmemesinin nedeni, normal olarak algıladığımız kütlesel çeki alanlarının çok zayıf oluşudur. Ancak, daha önce sözü edilen tekillik teoremleri, en az iki durumda, kara deliklerde ve büyük patlamada, çekim alanının çok şiddetli olacağına işaret ediyor. Böylesi şiddetli alanlarda, tanecik mekaniğinin etkileri önemli olmalı. Böylece, bir anlamda, klasik genel görelik, sonsuz yoğunlukta noktalar öngörmekle aslında kendi yıkılışının haberini veriyor, nasıl ki klasik (yani taneciksiz) mekanik, atomların sonsuz yoğunluğa çökeceğini ileri sürerek kendi yıkılışını öngördü. Henüz, genel göreliği ve tanecik mekaniğini birleştiren tam, tutarlı bir kuramımız yok, ama böyle bir kuramın taşıması gereken özelliklerin bir bölümünü biliyoruz. Bunların kara delikler ve büyük patlama için ne anlama geldiğini kitabımızın daha ileri bölümlerinde göreceğiz. Ama şimdilik, yakın zamanlardaki, doğanın öbür kuvvetlerine ilişkin anlayışlarımızı tek bir tanecik kuramında birleştirme çabalarına dönelim.

Yukarıdaki alıntı şu kitaptan alındı:
Stephan W. Hawking. Zamanın Kısa Tarihi - Büyük Patlamadan Kara Deliklere-.
Sayfa 82-88. Milliyet Yayınları 82, ISBN 975-506-006-C. Baskının yeri ve tarihi kitapta belirtilmemiş. İnglizce orijinal 1988'de, New York'ta basılmış.

Fizikte kaydedilen ilerleme ve yeni tartışmalar (stringler, uzay yapısıyla yeni buluşlar vs) olmakla birlikte bu tartışmaların mantığını (ve günlük mantığımızın yetersizliğini) anlamak için, bence okumaya son derece değer bir kitap.

Tıklayın: önceki sayfa